-

理学院何佳清团队在science发表高熵热电材料研究论文
-
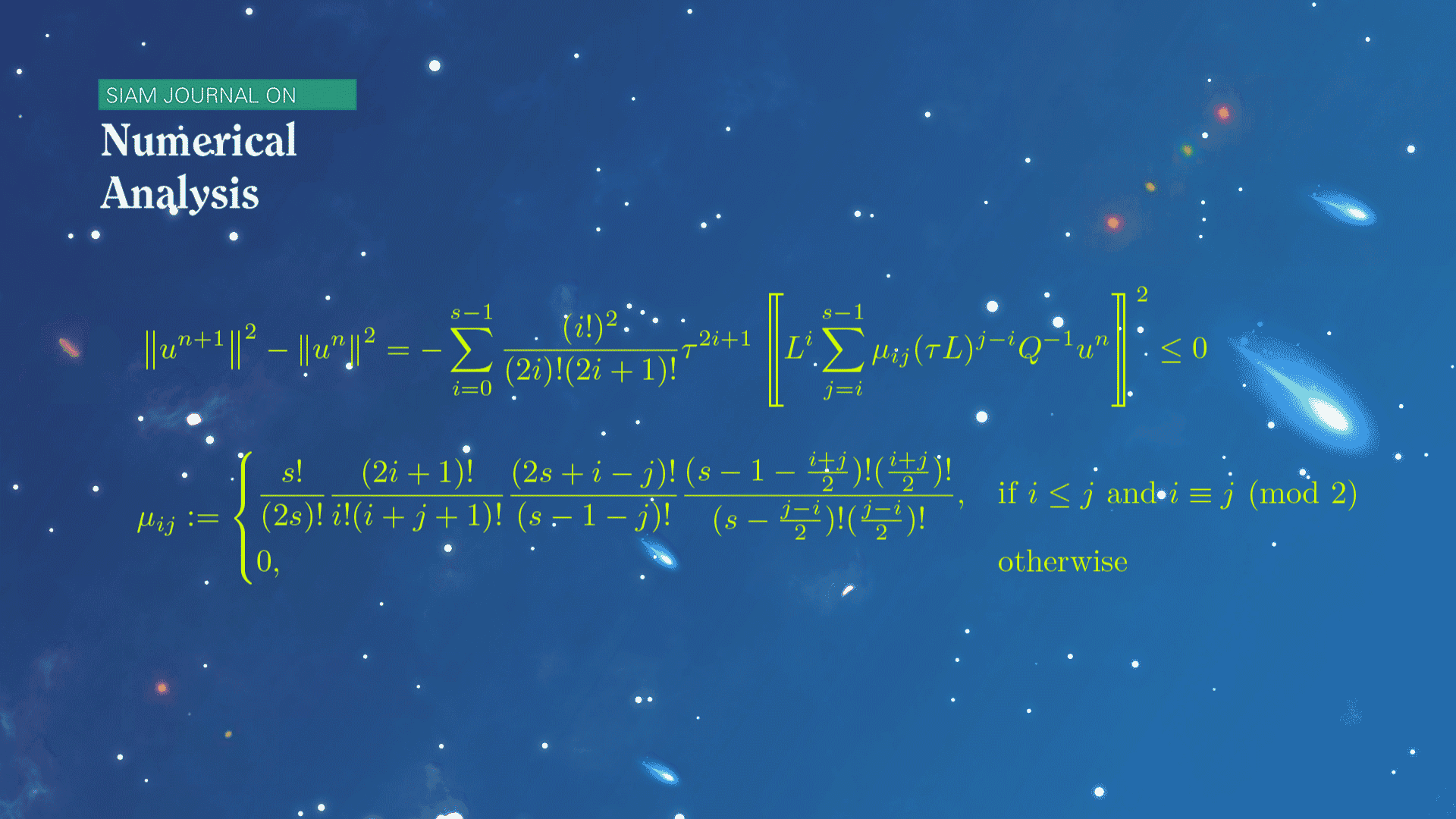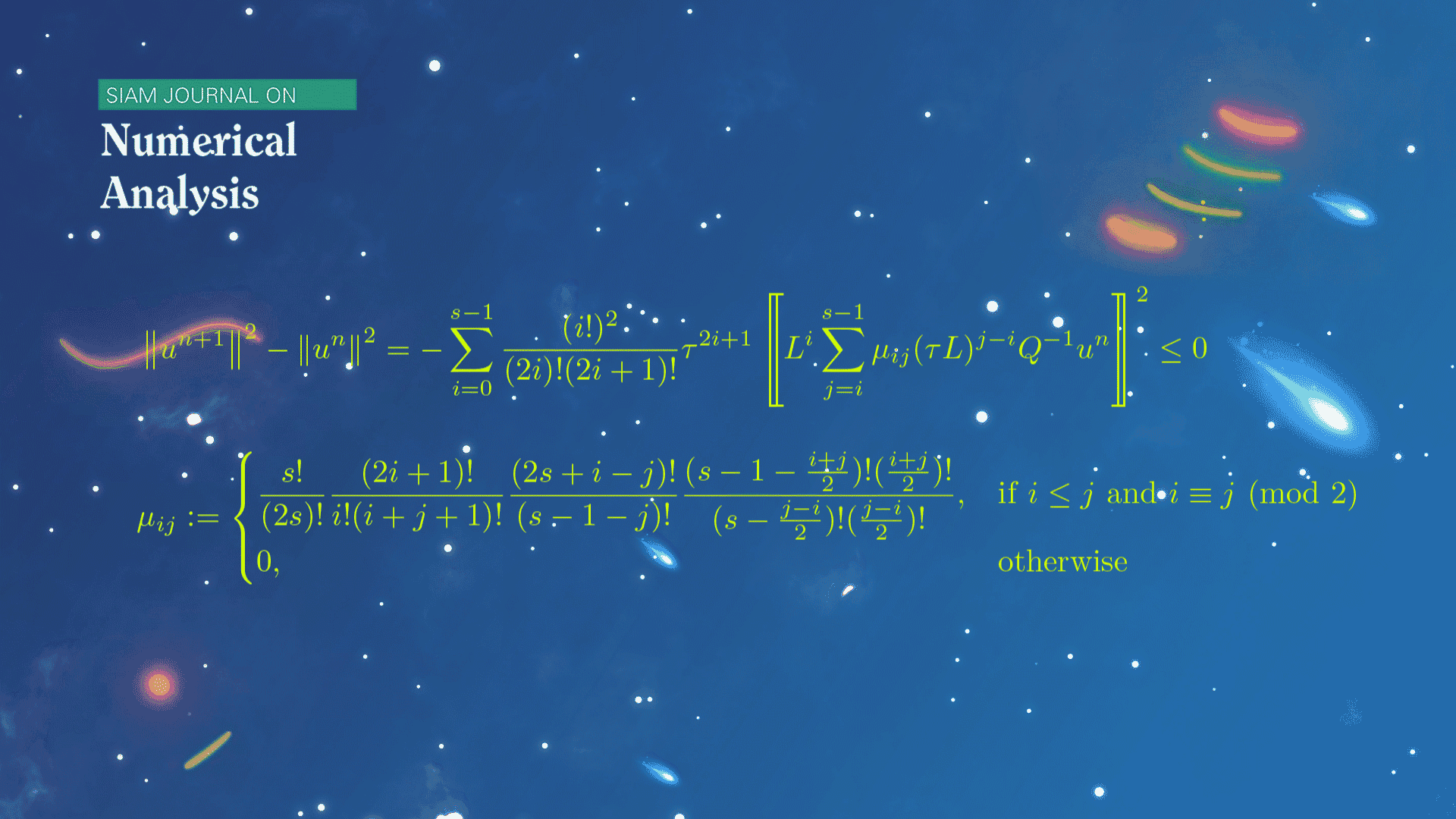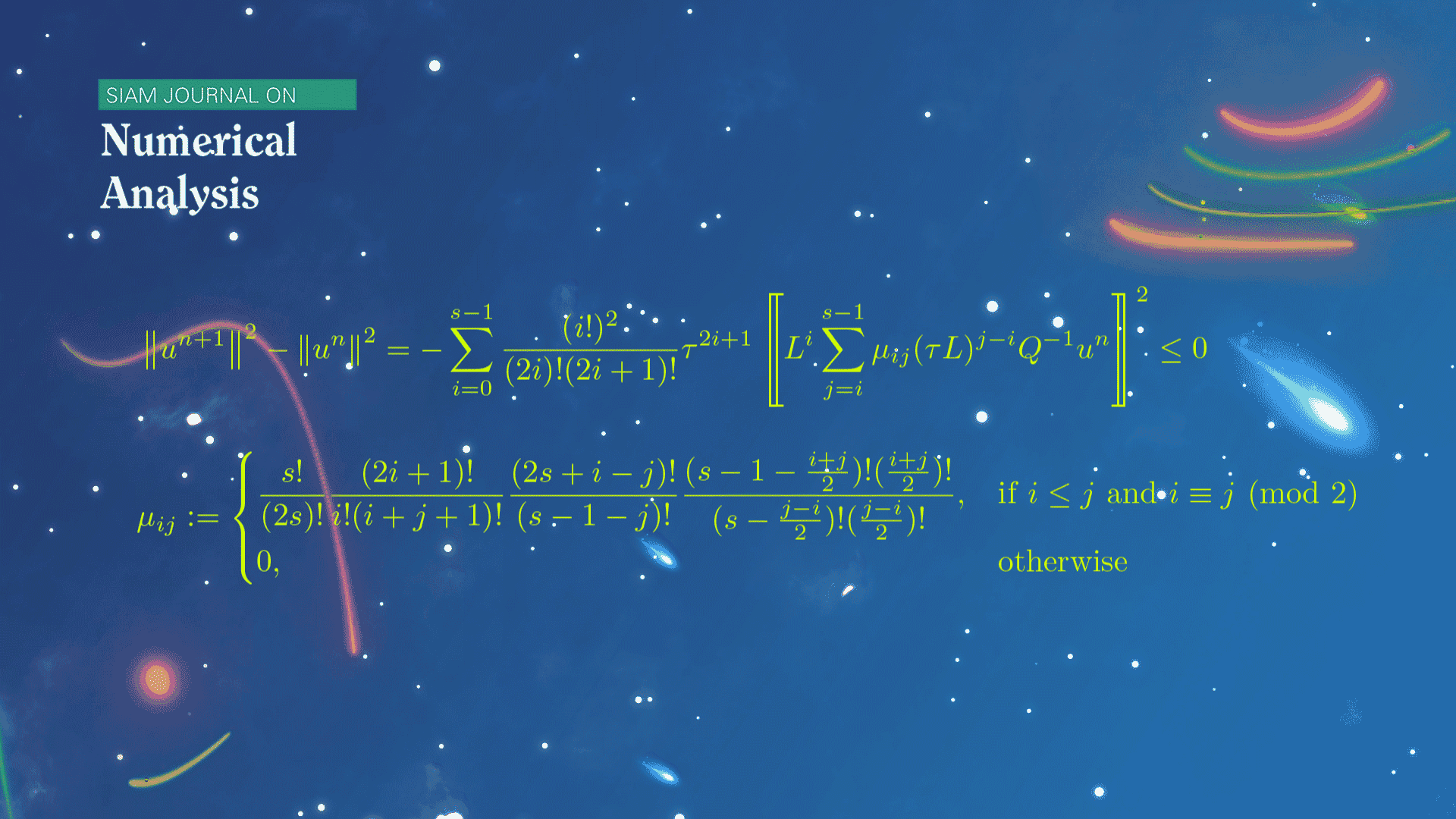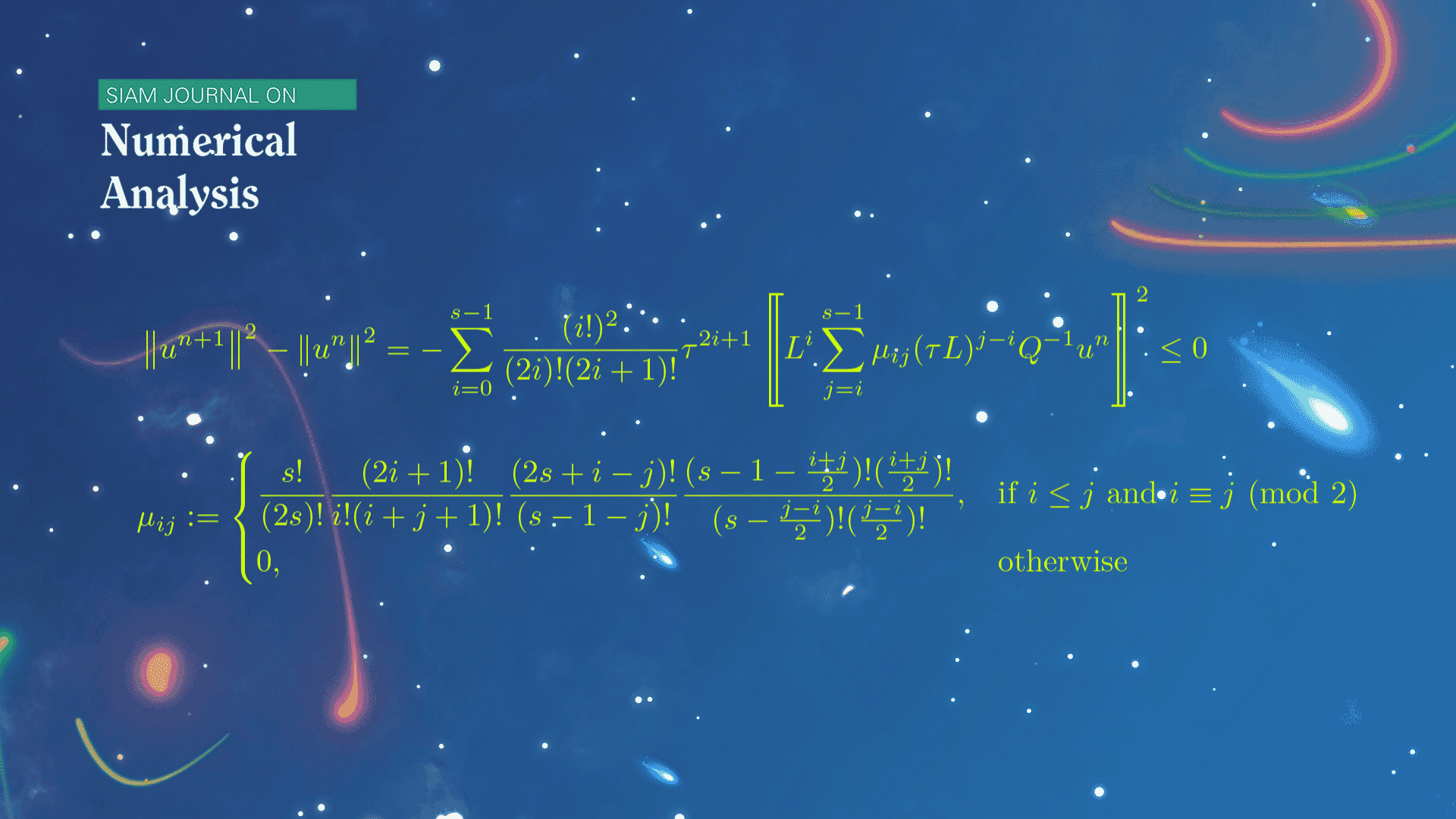
数学系本科生魏元哲等在龙格-库塔(Runge-Kutta)方法的稳定性研究方面取得新进展
-

前沿灼见向未来——“化学反应的量子特性”学术报告会在南科大召开
-

理学院范靖云课题组关于“复数的根本地位”的研究成果入选2022年国际物理学十大进展
-

Nature+1!化学系刘心元团队在立体汇聚式N-烷基化领域中取得重要进展
-
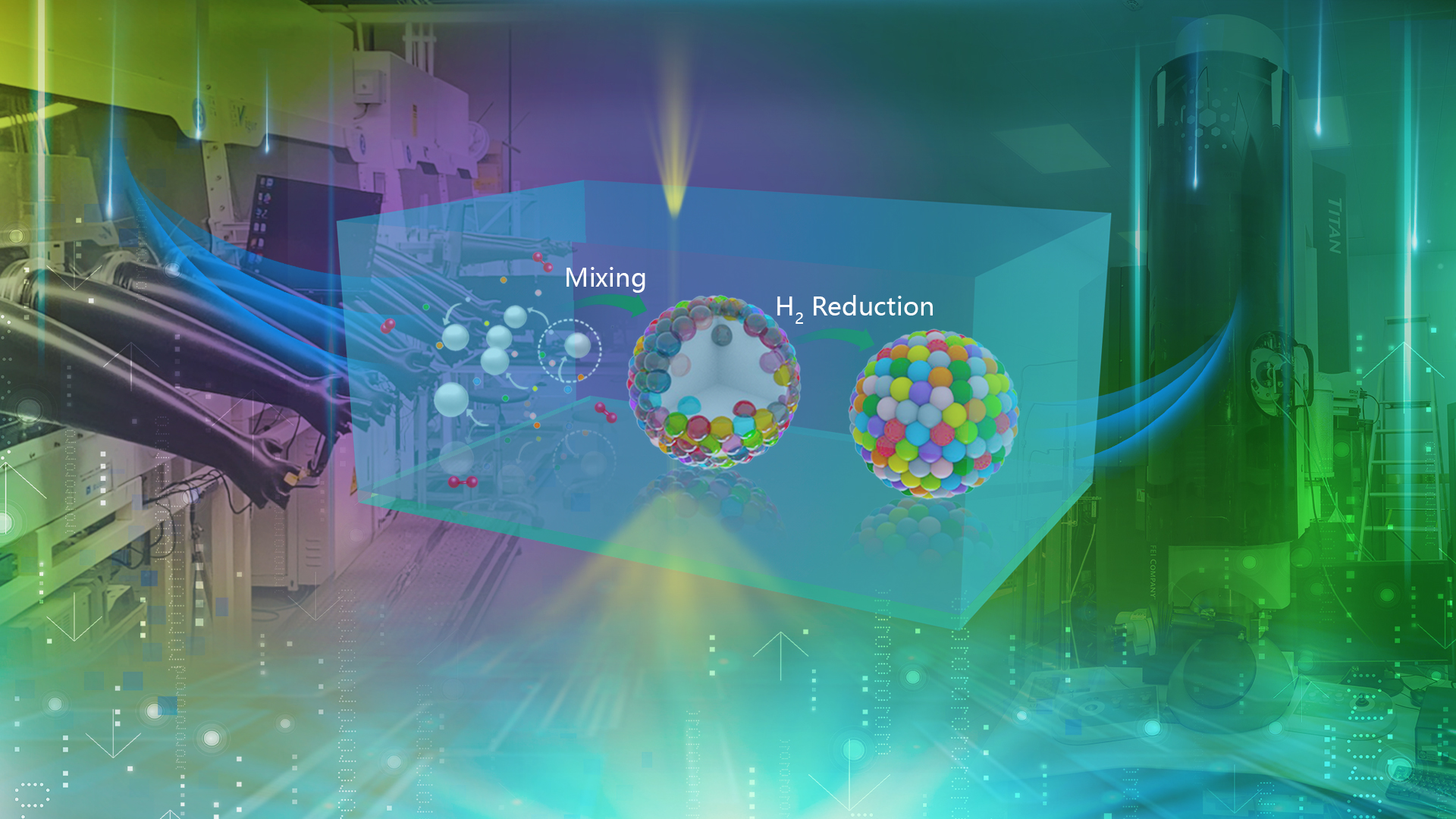
理学院林君浩团队合作在Nature发表有关高熵合金纳米颗粒合成与生长机理的研究成果
-

理学院刘柳团队在Science发文揭秘反电子态双亲性卡宾
-
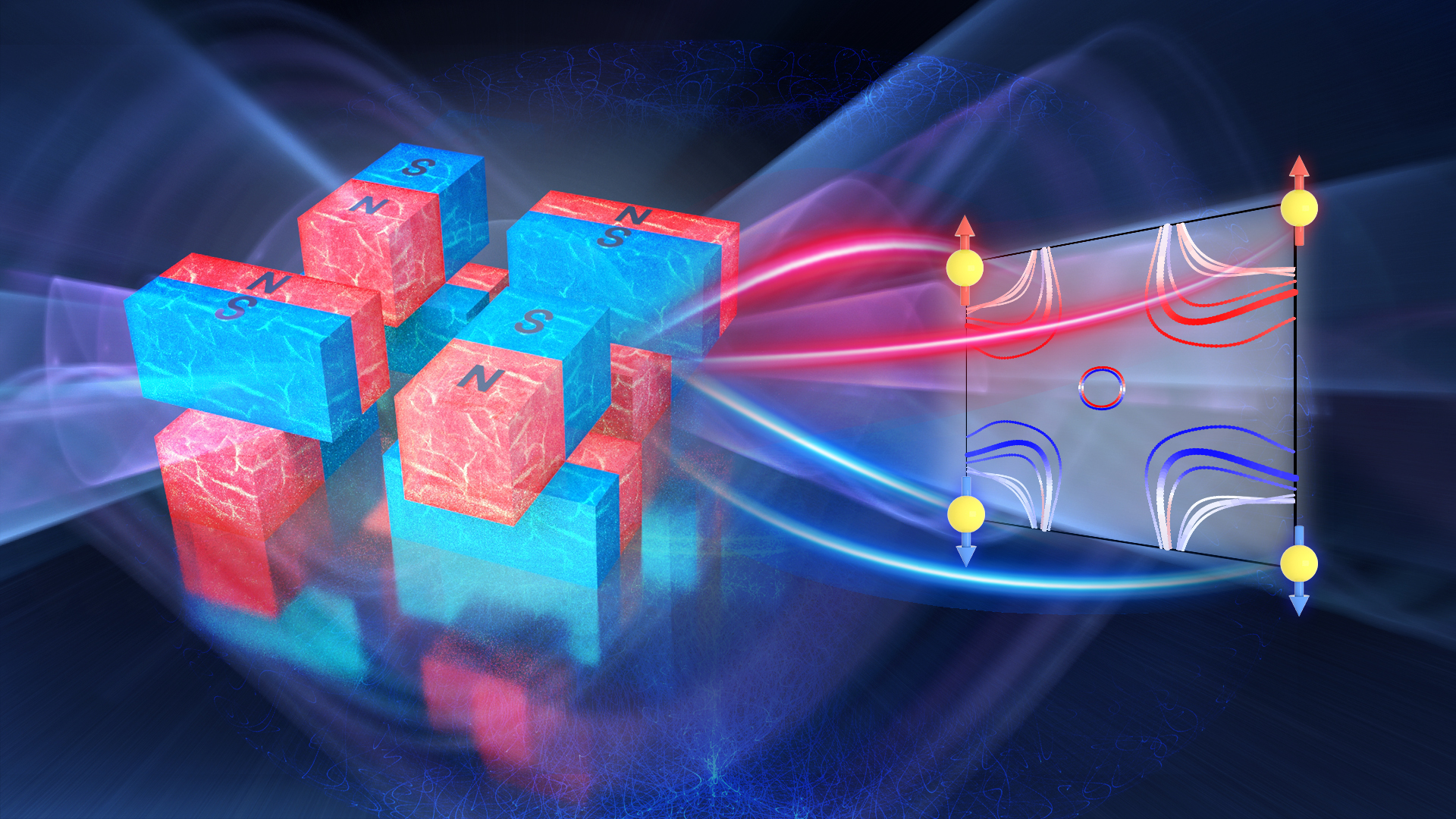
理学院刘畅、刘奇航课题组在Nature发表反铁磁材料自旋劈裂行为的研究成果
-

杨学明院士团队合作发现首例分子高激发态的漫游反应通道 成果登上Science
-

南科大何佳清团队通过捕获的空穴释放和赝纳米结构巧获高性能热电材料
-

南科大林君浩课题组合作首次合成二维全有机钙钛矿晶体,揭示其超低电子剂量有机官能团结构表征
-

南科大科研团队高温超导研究取得重大突破 发现常压下镍氧化物的高温超导电性
-

理学院物理系刘奇航课题组在自旋空间群预言的非常规磁振子研究中取得进展
-

“自由基不对称催化”的关键一步,南科大刘心元团队在Science发表最新成果
-

当金属邂逅轮烯,南科大夏海平团队Nature现化学之美
-
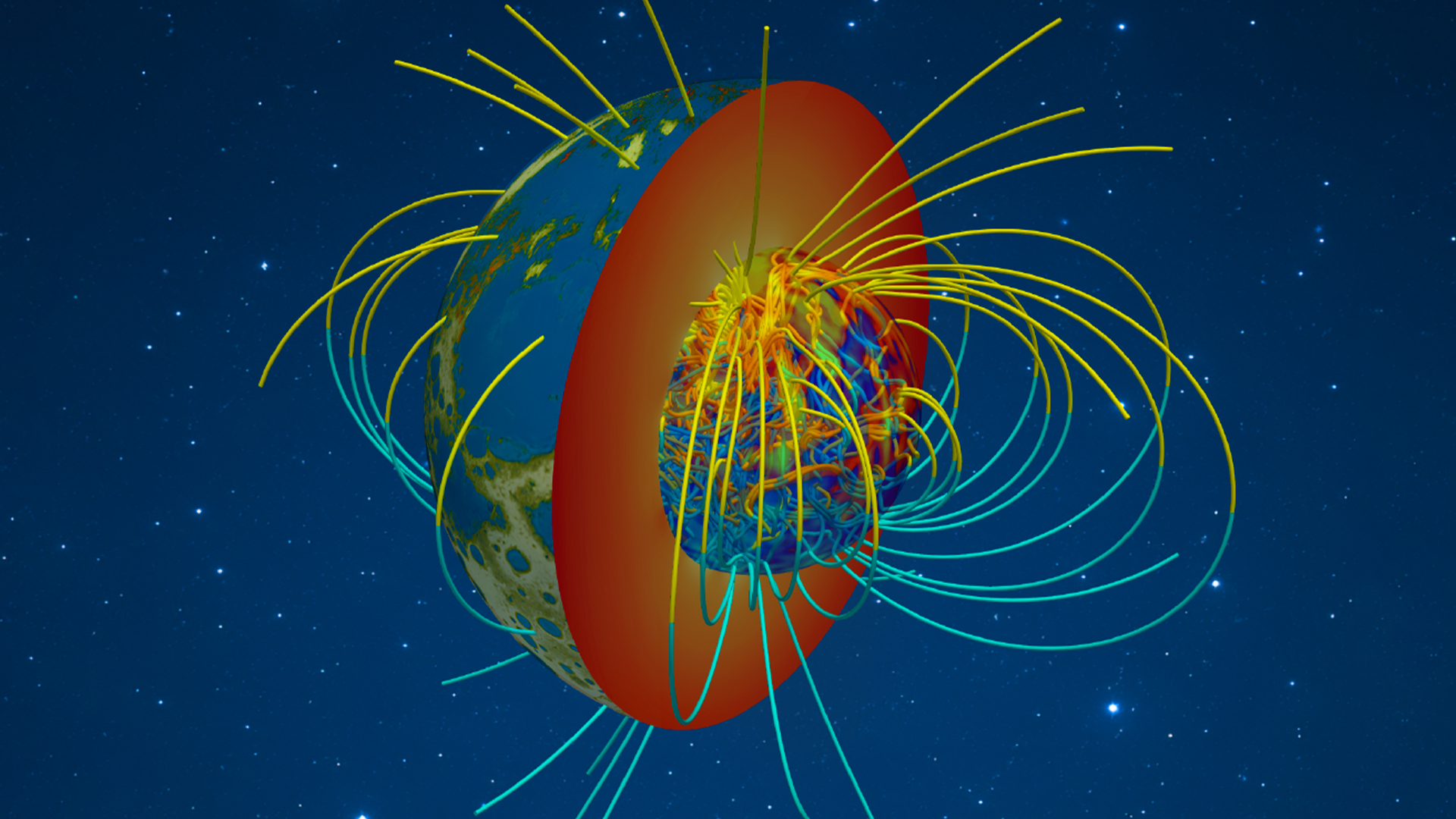
“无黏发电机”模拟实现!南科大林玉峰团队Nature发文揭示早期地球磁场产生机制